Neural Network-01 Batch Hard and Semi-Hard Triplet Loss

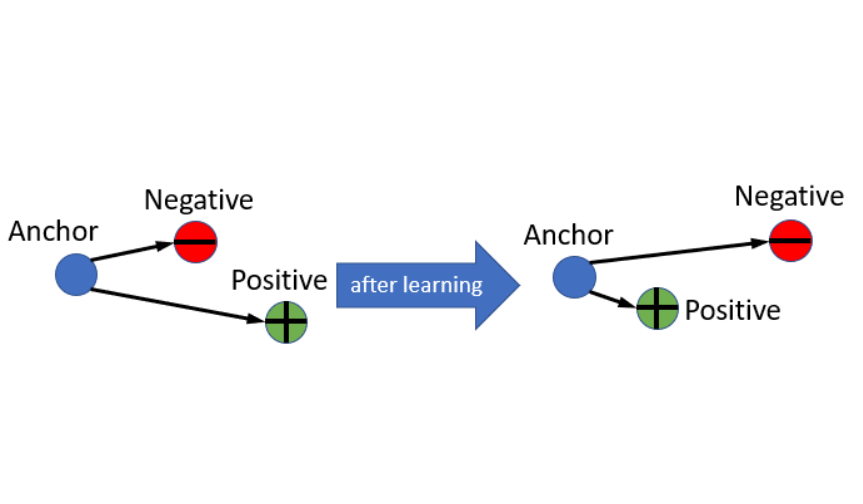
Triplet Loss

Triplet Loss的介紹，相信在網路上已經有許多例子了，用途跟作用這邊就不多作介紹，將triplet的公式列出來，直接進入正題：

$$ {\mathcal{L_{triplet}}=\max{(\sum_{i=1}^N[||f^a_i - f^p_i||_2^2-||f^a_i - f^n_i||_2^2 + margin] ,\ 0)}} $$

這邊會依序測試兩種不一樣的Triplet來計算Triplet Loss，分別是：

1. Batch Hard
2. Semihard

Sample Data

首先要先Sample出兩個不同的Embedding資料，直接使用numpy的random來產生兩個隨機的Embedding。
這邊設定Batch Size是64、每筆資料的維度為1024、Margin設定為0.3、另外Label這邊設定是每筆都是獨立的資料，所以每一筆資料對應一個label：

import numpy as np

batch = 64
emb_dim = 1024

np.random.seed(1234)
emb1 = np.random.rand(batch,emb_dim).astype(np.float32)
np.random.seed(2345)
emb2 = np.random.rand(batch,emb_dim).astype(np.float32)
margin = 0.3
labels = np.arange(batch)

Triplet Loss (Batch Hard)

直接將最小的AN距離減掉最大的AP距離加上margin，此為Batch Hard的Triplet Loss。

Distance Metric

在Tensorflow Addons原始碼中使用square再加起來等價於$XX^T$取對角的element，不過不確定跟目前使用的方法計算複雜度的差距：

# 矩陣相乘再取對角的element
xx = np.matmul(x, np.transpose(x))
xx = np.diag(xx)
# 使用square再根據axix=1相加
xx = tf.math.reduce_sum(tf.math.square(x), axis=[1], keepdims=True)

針對一個batch所有的資料兩兩計算，形成一個Batch*Batch的metric：

這裡計算每一筆的距離，回傳的是一個shape=(batch, batch)的metric：

def np_distance_metric(embedding, squared=True):
    """
    Args:
       embedding: float32, with shape [n, d], (batch_size, d)
    Returns:
        dist: float32, with shape [m, n], (batch_size, batch_size)
    """
    # |x-y|^2 = x^2 - 2xy + y^2
    xy = np.matmul(embedding, np.transpose(embedding))
    square_norm = np.diag(xy)
    xx = np.expand_dims(square_norm, 0)
    yy = np.expand_dims(square_norm, 1)
    distances = np.add(xx, yy) - 2.0 * xy
    '''
    (batch_size,1)-(batch_size,batch_size): Equivalent to each column operation
    (batch_size,batch_size)+(1,batch_size): Equivalent to each row operation
    '''
    # Deal with numerical inaccuracies. Set small negatives to zero.
    distances = np.maximum(distances, 0.0)
    # Get the mask where the zero distances are at.
    error_mask = np.less_equal(distances, 0.0).astype(np.float32)

    if not squared:
        # Because the gradient of sqrt is infinite when distances == 0.0 (ex: on the diagonal)
        # we need to add a small epsilon where distances == 0.0
        distances = np.sqrt(distances + error_mask * 1e-16)

    # Undo conditionally adding 1e-16.
    distances = np.multiply(distances, np.logical_not(error_mask),)

    num_data = np.shape(embedding)[0]
    # Explicitly set diagonals to zero.
    mask_offdiagonals = np.ones_like(distances) - np.diag(np.ones([num_data]))
    distances = np.multiply(distances, mask_offdiagonals)
    return distances

Mask

_masked_minimum做的簡而言之就是將乘上mask後的data中根據dim取其最小值，具體步驟是：

首先將每筆資料對應的最大值選取出來，命名為：axis_maximums，將Distance Metric減掉這個最大值(axis_maximums)，再乘上mask選取出需要比較的數值，接下來根據dim取出對應行或列中最小值，最後再將axis_maximum加回去就可以得到需要的結果，然後需要注意這邊有keepdims，所以會是(batch, 1)的形式。

具體的實現過程為：

def np_masked_minimum(data, mask, dim=1):
    """Computes the axis wise minimum over chosen elements.
    Args:
      data: float32, with shape [n, m], (batch_size, batch_size)
      mask: boolean, with shape [n, m], (batch_size, batch_size)
      dim: int, the dimension which want to compute the minimum.
    Returns:
      masked_minimums: float32, with shape [n, 1], (batch_size, batch_size)
    """
    axis_maximums = np.max(data, dim, keepdims=True)
    masked_minimums = (np.min(np.multiply(data - axis_maximums, mask), dim, keepdims=True) + axis_maximums)
    return masked_minimums

_masked_maximum做的事情和上面一樣，不過得到的為最大值：

def np_masked_maximum(data, mask, dim=1):
    """Computes the axis wise maximum over chosen elements.
    Args:
      data: float32, with shape [n, m], (batch_size, batch_size)
      mask: boolean, with shape [n, m], (batch_size, batch_size)
      dim: int, the dimension over which to compute the maximum.
    Returns:
      masked_maximums: N-D `Tensor`.
    """
    axis_minimums = tf.math.reduce_min(data, dim, keepdims=True)
    masked_maximums = (tf.math.reduce_max(tf.math.multiply(data - axis_minimums, mask), dim, keepdims=True) + axis_minimums)
    return masked_maximums

定義出以上function之後，就可以開始進行整個Triplet Loss的計算。

Batch Hard

首先先算出pairwise的距離矩陣pdist_matrix，再利用labels計算出row index和column index對應的embedding是否有相同的label(adjacency)，相反可以得出不同的label(adjacency_not)。

如此就可以得到negative所在的mask和positive所在的mask，利用前面的mask function找出hardest的negative，同理利用前面的adjacency再去掉相同index的element就可以得到positive的mask，也就是得到hardest的positive。

有了hardest的positive跟negative就可以直接帶入triplet的公式：

def np_triplet_batch_hard(labels, embedding, margin, soft):
  	'''
    batch all triplet loss of a batch
    ------------------------------------
    Args:
        labels:     Label Data, shape = (batch_size,1)
        embedding:  embedding vector, shape = (batch_size, vector_size)
        margin:     margin, scalar
        soft::     	use log1p or not, boolean
    Returns:
        triplet_loss: scalar, for one batch
    '''
    # Reshape label tensor to [batch_size, 1].
    lshape = np.shape(labels)
    labels = np.reshape(labels, [lshape[0], 1])
    # Build pairwise squared distance matrix.
    pdist_matrix = _distance_metric(embedding, squared=True)

    # Build pairwise binary adjacency matrix.
    adjacency = np.equal(labels, tf.transpose(labels)).astype(np.float32)
    # Invert so we can select negatives only.
    adjacency_not = np.logical_not(adjacency).astype(np.float32)

    # hard negatives: smallest D_an.
    hard_negatives = _masked_minimum(pdist_matrix, adjacency_not)

    batch_size = np.size(labels)
    mask_positives = adjacency - np.diag(np.ones([batch_size]))
    # hard positives: largest D_ap.
    hard_positives = _masked_maximum(pdist_matrix, mask_positives)
    if soft:
        triplet_loss = np.log1p(np.exp(hard_positives - hard_negatives))
    else:
        triplet_loss = np.maximum(hard_positives - hard_negatives + margin, 0.0)

    # Get final mean triplet loss
    triplet_loss = np.mean(triplet_loss)

    return triplet_loss

Triplet Loss (Semi-Hard)

前面定義出了Batch Hard的Triplet Loss是怎麼運作的，接下來要介紹什麼是Semi-Hard的Tirplet，簡而言之就是要找那些AN>AP但<margin的pair。

這裡分成5個部分來分別介紹。

Distance Metric

和前面一樣先計算出pdist_matrix，和相應的adjacency mask跟adjacency_not mask：

pdist_matrix = _distance_metric(embedding, squared=True)

adjacency = np.equal(labels, tf.transpose(labels)).astype(np.float32)
adjacency_not = np.logical_not(adjacency).astype(np.float32)

negatives_outside

將pdist_matrix複製batch次，會得到pdist_matrix_tile，其shape為(batch*batch, batch)，這是為了之後要挑出Semi-Hard的triplet pair而計算：

pdist_matrix_tile = tf.tile(pdist_matrix, [batch_size, 1])

同樣將adjacency_not複製batch次，並且將pdist_matrix根據row展開成一列其shape為(batch*batch, 1)，讓pdist_matrix_tile中每一個element依序和展開的pdist_matrix相比，大於為Ture、反之False，最後再和batch倍的adjacency_not(為negative的所在)做and運算，例子如下：

'''
np.reshape(np.transpose(pdist_matrix), [-1, 1])
------------------------------------
ex. pdist_matrix = [[ 0. 11. 11.]
                    [11.  0. 24.]
                    [11. 24.  0.]]
轉換成(batch*batch,1):
[[ 0.], [11.], [11.], [11.], [ 0.], [24.], [11.], [24.], [ 0.]]

依序和展開的`pdist_matrix`相比
np.greater(pdist_matrix_tile, np.reshape(np.transpose(pdist_matrix), [-1, 1]))
------------------------------------
[[False  True  True]
 [False False  True]
 [False  True False]
 [False False False]
 [ True False  True]
 [False False False]
 [False False False]
 [False False False]
 [ True  True False]]
 
 np.logical_and(a, b)
------------------------------------
[[False  True False]	[[False  True  True]	[[False  True False]
 [ True False  True]	 [False False  True]	 [False False  True]
 [False  True False]	 [False  True False]	 [False  True False]
 [False  True False]	 [False False False]	 [False False False]
 [ True False  True] and [ True False  True]  =  [ True False  True]
 [False  True False]	 [False False False]	 [False False False]
 [False  True False]	 [False False False]	 [False False False]
 [ True False  True]	 [False False False]	 [False False False]
 [False  True False]]	 [ True  True False]]	 [False  True False]]
 '''
a = np.tile(adjacency_not, [batch_size, 1])
b = np.greater(pdist_matrix_tile, np.reshape(np.transpose(pdist_matrix), [-1, 1]))
mask = np.logical_and(a, b)

這邊將pdist_matrix中的batch*batch展開，將每一筆當作AP和對應的row去比較(第一筆為row 1對column 1的距離，讓他對第一個row比較，如下圖)，所以這邊評估在每個row中哪些比他本身更大，更大的作為True。

(1.1對1.all比較，1.2對2.all比較，…
2.1對1.all比較，2.2對2.all比較，…
3.1對1.all比較，3.2對2.all比較，…)

接下來透過tile過的adjacency_not，把屬於不同label並且距離大於AP(pdist_matrix中每個element)的都挑選出來了。

接合前面的np_masked_minimum function我們可以得到AN的Semi-Hard的候選清單，也就是AN>AP的情況下最小的AN：

# negatives_outside: smallest D_an where D_an > D_ap.
negatives_outside = np.reshape(
np_masked_minimum(pdist_matrix_tile, mask), [batch_size, batch_size]
)
negatives_outside = np.transpose(negatives_outside)

negatives_inside

以上滿足了AP<AN的狀況下找尋可計算pair，但有可能會存在AN<AP的時候，這個時候要找最遠的AN，和AP比較，也就是easy negatives：

# negatives_inside: largest D_an.
negatives_inside = np.tile(np_masked_maximum(pdist_matrix, adjacency_not), [1, batch_size])

semi_hard_negatives

將前面的mask，也就是AN>AP的情況下是否擁有的AN，做reduce_sum。換句話說就是將AN>AP的狀況下存在AN的element為True (也就是semi-hard的部分)，使用negatives_outside的距離，反之用negatives_inside：

'''
np.where(condition, x, y):
if condition:
	return x 
else:
	return y
'''
mask_final = np.reshape(np.greater(np.sum(mask.astype(np.float32), 1, keepdims=True),0.0), [batch_size, batch_size])
mask_final = np.transpose(mask_final)

semi_hard_negatives = np.where(mask_final, negatives_outside, negatives_inside)

最後在滿足mask_final的情況下選擇negatives_outside和negatives_inside，作為AN來計算Triplet Loss，得到loss_mat。

Semi-Hard Triplet

因為在對角線部分為anchor對anchor的距離，這邊需要將它過濾掉，因為不是這邊需要的，所以算出label相同的mask之後減掉對角線，就可以找到positive的位置，將前面的loss_mat乘上這邊的mask，算總和後除以positive數量，就可以得到最後的triplet loss：

loss_mat = np.add(margin, pdist_matrix - semi_hard_negatives)

mask_positives = adjacency.astype(np.float32) - np.diag(np.ones([batch_size]))

# Take all positive pairs except the diagonal.
num_positives = tf.math.reduce_sum(mask_positives)

triplet_loss = tf.math.truediv(
  tf.math.reduce_sum(
    tf.math.maximum(tf.math.multiply(loss_mat, mask_positives), 0.0)
  ),
  num_positives,
)

Code Link

以上所有的code都是在Google Colab上面執行，版本為2.2.0。

Github：NeuralNetwork-01 Batch Hard and Semi-Hard Triplet Loss

參考資料

Triplet-Loss原理及其实现